In this post we will try to implement gradient descent approach to solve logistic regression problem.
Please note this is mainly for educational purpose and the aim here is to learn. If you want to “just apply” logistic regression in julia please check out this one
Lets start with basic background.
Logistic regression is a mathematical model serving to predict binary outcome (here we consider binary case) based on set of predictors. Binary outcome (meaning outcome with two possible values, like physiognomical gender spam/not spam email or fraud/legit transaction) is very often called target variable and predictors can be also called features. The latter name is much more intuitive as it is closer to Earth, so to say, it suggests we deal with some sort of objects with known features and we try to predict binary feature that is unknown at the time of prediction. The main idea is to predict the target given set of features based on some training data. Training data is a set of objects for which we know the true target.
So our task is to derive a function that will later serve as a 0/1 labelling machine – mechanism to produce (hopefully) correct target for given object described with features. The class of functions we choose to derive the target is called the model. Such a class is parametrized with set of parameters and the task of learning is in fact to derive these parameters to let our model perform well. Performing well is on the other hand measured with yet another function called goal function. The goal function is what we optimize when we learn parameters for a model. It involves model parameters and training data. It is a function of model parameters and training data with known labels. So the problem of machine learning can be (ignorantly of course) reduce to the problem of estimating set of parameters of given class of functions (model) to minimize given goal function.
Many different models exist with various goal functions to optimize. Today we will focus on one specific model called logisitic regression. We will present some basic concepts, formalize data a little bit and formulate goal function that will happen to be convex and differentiable (in practice it means the underlying optimization problem is “easy”).
As we stated before we will need the following components in our garage.
– training data. It is a set of observations/objects you have and you want to learn from. Each observation/object is defined as a set of numbers, each number has a meaning. We model our objects as vectors, so lets assume training set is a set of \(N\) vectors \(x \in \mathcal{R}^D\), where \(\mathcal{R}\) is the set of real numbers and \(D\) is dimensionality of the vectors. It is basically just number of features object is described with. We assume each object is described with the same number of features \(D\).
– set of labels. For each training example there is corresponding binary label. We can model all labels in one structure, vector again. So lets assume target vector to be \(y \in \{0,1\}^N\)
– logistic regression model. This is our model, lets take a look
\[
f(x ,(\beta,\omega)) = \frac{1}{1 + \exp(-(\beta + \omega x))}
\]
where \(x \in \mathcal{R}^D\) is \(D\)-dimensional vector representing object under prediction, and \((\beta, \omega)\) is set of model parameters. \(\beta\) is a scalar while \(\omega\) is \(D\)-dimensional vector of coefficients. Please note that each coefficient corresponds to single feature, so \(\omega x\) can be seen as weighted sum of features of \(x\) with \(\beta\) as free parameter. To get the basic intuition about the reason for such a choice lets for now blackbox expression \((\beta + \omega x)\) into \(z\) and think of
\[
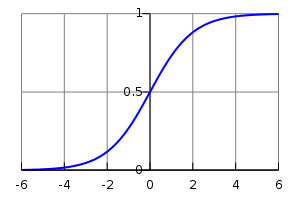
f(z) = \frac{1}{1 + \exp(-z)}
\]
this function is called logistic function and its plot looks like this:
Please note the following properties. The smaller the \(z\) the closer \(f\) to 1 and analogically, The greater the \(z\) the closer \(f\) to 0 (note minus sign in formula in case of doubts). Ok now we can unbox \(z\) again and think of it as weighted sum again \((\beta + \omega x)\). We can also conclude that our model will predict values close to 1 whenever aforementioned weighted sum is high negative number with the opposite holding as well: if weighted sum is high positive number prediction will be close to 0. That can already provide basic intuition of what we will try to do here. We need to set model parameters in a way that model predictions are close to correct, namely for 0-labeled data we want weighted sum to be as positive as possible and for 1-labeled data we wish the opposite. And that brings us to the next puzzle
– goal function: logistic regression optimization problem. The next puzzle is the goal function we wish to optimize. It is going to reflect our intuition of what “learning” means. Once again, what we need is a set of parameters that makes our predictions close to real labels. Common way of representing that is by using likelihood function given by the formula
\[
J((\beta, \omega), X,y) = \prod_{i = 1}^{N} f(x_{i}, (\beta,\omega))^{y_{i}} (1 – f(x_{i},(\beta,\omega)))^{(1 – y_{i})}
\]
Even though formula look scary it can be easily explained in an ELI5 fashion. First of all for any single index \(i\) we in fact deal with either \(f(x_{i}, (\beta,\omega))^{y_{i}}\) or \((1 – f(x_{i},(\beta,\omega)))^{(1 – y_{i})}\). If \(y_i = 0\) then first component vanish. if \(y_i = 1\) second one does.
Lets see what happens to \(f(x_{i}, (\beta,\omega))^{y_{i}}\) depending on value of \(y_i\)
– \(y_i = 1\). If prediction \(f(x_{i}, (\beta,\omega))\) is close to 1 it contributes to \(J\) more.
– \(y_i = 0\). If prediction \(f(x_{i}, (\beta,\omega))\) is close to 0 it contributes to \(J\) more.
Then two polars of function \(J\) are 0 and 1. Zero when all predictions are incorrect and 1 in case of correct predictions for all traning data points. Our task is then to maximize \(J\) in the parameter space. The convention in scientific world is to consider any optimization problem as minimization problem so in fact we will try to minimize \(-J((\beta, \omega), X,y)\). Moreover for mathematical convenience (and practical reasons) we will in fact minimize \(- \log(J((\beta, \omega), X,y))\), The practical reason can be easily provided: If number of data points is high enough product of many (potentially) small numbers may cause problems with computational precision.
Having all that we can now wrap our problem in function optimization problem with our function to be optimized given by:
\[
\hat{J} = -\log(J(\theta, X,y)) = – \sum_{i = 1}^{N} y_{i} \log(f(x_{i}, (\beta,\omega))) + (1 – y_{i}) \log(1 – f(x_{i},(\beta,\omega)))
\]
Well, believe it or not but our \(\hat{J}\) function is convex function of \((\beta, \omega)\). Proof of that is quite long and it uses the fact that linear combination of convex functions is also convex. ( so in fact proof reduces to showing convexity of each component of \(\hat{J}\) )
In the context of optimization, goal function convexity ensures the following: if any local solution is found, it is also global solution to our problem. This is what makes our problem “easy”.
After taking a deep breath we can now try to solve it. For solving that type of problems people use gradient descent method. The idea is to start from random point on a function surface and move towards gradient at given point by certain step \(\alpha\). One can imagine climbing the hill in a locally greedy fashion. Gradient descent method can be described by repeating the following routine:
\[
\forall_{i} \omega_{i} = \omega_{i} – \alpha \frac{\mathrm{d}\hat{J}}{\mathrm{d}\omega_{i}} \hat{J}
\]
\[
\beta = \beta – \alpha \frac{\mathrm{d}\hat{J}}{\mathrm{d}\beta} \hat{J}
\]
until convergence
Algorithm will iteratively follow the gradient of function being optimized and update current solution with step \(\alpha\). One last piece we miss to implement the algorithm in Julia is the formula for derivatives themselves. This is the matter of calculus
\[
\frac{\mathrm{d}\hat{J}}{\mathrm{d}\omega_{i}} \hat{J} = \dots = \sum_{j}^{N} ( f(x_{j}, (\beta,\omega)) – y_{j} ) x_{ji}
\]
\[
\frac{\mathrm{d}\hat{J}}{\mathrm{d}\beta} \hat{J} = \dots = \sum_{j}^{N} ( f(x_{j}, (\beta,\omega)) – y_{j} )
\]
To avoid headaches I ommited details of that basic (strictly technical) derivation with dots…
Julia implementation
Lets now list components we need in our code:
- Main loop. We need main loop where parameters update takes place
- Update functions. We need functions to update model parameters in each iteration
- Goal function. We will need goal function value in each iteration
- Convergence criterion function (to stop the main loop at some point)
Lets enclose the main loop within one main function called “logistic_regression_learn” and add few helper functions. We will start with simple scaffolding code
function predict(data, model_params)
return 1.
end
function goal_function(omega::Array{Float64,2}, beta::Float64, data::Array{Float64,2}, labels::Array{Float64,1})
return 0
end
function convergence(omega::Array{Float64,2}, beta::Float64, data::Array{Float64,2}, labels::Array{Float64,1}, prevJ::Float64, epsilon::Float64)
return true
end
function update_params(omega::Array{Float64,2}, beta::Float64,data::Array{Float64,2}, labels::Array{Float64,1}, alpha::Float64)
omega,beta
end
function logistic_regression_learn(data::Array{Float64,2}, labels::Array{Float64,1}, params::Dict{Symbol,Float64})
omega = zeros(Float64, size(data,2),1)
beta = 0.0
J = Inf
current_iter = 0
alpha_step, epsilon, max_iter = params[:alpha], params[:eps], params[:max_iter]
while !convergence(omega, beta, data, labels, J, epsilon) && current_iter < max_iter
J = goal_function(omega, beta, data, labels)
omega, beta = update_params(omega, beta, data, labels, alpha_step)
current_iter += 1
end
model_params = Dict();
model_params[:omega] = omega; model_params[:beta] = beta;
return model_params
end
Lets comment logistic_regression_learn first. Its main goal is to return model parameters that solve the logistic regression problem. Input argument Data represents training data points. Labels represent corresponding binary labels. And last argument params is a dictionary containing all parameters the learning method requires (like gradient descent alpha step, maximal iterations number and epsilon that is needed to establish convergence).
First few lines within main function loop (logistic_regression_learn) serve for initialization purpose. We will initialize all of our model (omega and beta) parameters to 0. J will represent current goal function value. We set it to Infinity to have the worst possible value at the beginning of the algorithm run [it ensures convergence returns false in 1st iteration]
Well, we now “only” need to do the boring job of mapping formulas into Julia code. Lets start with the easiest part, predict function – with the purpose to predict model output based on given input data and model parameters. It is just logistic function applied on weighted sum of input and model parameters.
function predict(data, model_params) 1.0 ./ (1.0 + exp(-data * model_params[:omega] - model_params[:beta])) end
Goal function now:
function goal_function(omega::Array{Float64,2}, beta::Float64, data::Array{Float64,2}, labels::Array{Float64,1})
f_partial = 1.0 ./ (1.0 + exp(-data * omega - beta))
result = -sum(labels .* log(f_partial) + (1.0 - labels) .* log(1.0 - f_partial))
return result
end
Few things to observe here. Most importantly, we implicitly chose certain convention here. We are going to treat data as an array where each row is a single observation. Another detail maybe is that we avoid computing f function twice and pre-compute it before and store up front (f_partial).
The code looks quite ok but it has its drawbacks that need attention: goal_function may produce NaN. Lets try to provoke it:
omega, beta = 750 *ones(1,1), 0. data, labels = transpose([[1.]]), [1.] unexpected = goal_function(omega, beta, data, labels)
Value of unexpected in that case is NaN. It is because
exp(-data * omega - beta)
is evaluated to 0 which implies f_partial being evaluated to 1 and finally log(1.0 – f_partial) is then evaluated to -Inf. Corresponding label is zero and so multiplication of 0 and -Inf results in NaN that is returned. But that is not really expected. Behaviour of * operator is problematic here. We need a function that won’t believe in artificial Infinity and instead of NaN produce 0. Lets define that function quickly
function _mult(a::Array{Float64,1},b::Array{Float64,2})
result = zeros(length(a))
both_non_zero_indicator = ((a .!= 0) & (b .!= 0))
result[both_non_zero_indicator[:]] = a[both_non_zero_indicator[:]] .* b[both_non_zero_indicator]
return result
end
Now we can rewrite goal function
function goal_function(omega::Array{Float64,2}, beta::Float64, data::Array{Float64,2}, labels::Array{Float64,1})
f_partial = 1.0 ./ (1.0 + exp(-data * omega - beta))
result = -sum(_mult(labels, log(f_partial)) + _mult((1.0 - labels), log(1.0 - f_partial)))
return result
end
Lets see now:
omega, beta = 750 *ones(1,1), 0. data, labels = transpose([[1.]]), [1.] result = goal_function(omega, beta, data, labels)
result is now “correctly” evaluated to 0 and that is the expected behavior. Uff. Lets grab another thing to work on: convergence criterion
We will use the most intuitive criterion and plan to stop iterating over whenever J “practically” stops changing (meaning we are probably very close to optimal solution). The “practically” part will be expressed by very small number that will be compared to J change after each iteration. Whenever J does not change by a number greater than epsilon, we stop iterating. The implementation could look like this:
function convergence(omega::Array{Float64,2}, beta::Float64, data::Array{Float64,2}, labels::Array{Float64,1}, prevJ::Float64, epsilon::Float64)
currJ = goal_function(omega, beta, data, labels)
return abs(prevJ - currJ) < epsilon
end
Additionally we will have the plan B to stop iterating whenever maximal number of iterations is reached (that could indicate wrong alpha choice).
The last puzzle is the update function. Lets make a first attempt to (very) naively map formulas into Julia:
function update_params(omega::Array{Float64,2}, beta::Float64,data::Array{Float64,2}, labels::Array{Float64,1}, alpha::Float64)
updated_omega = zeros(Float64, length(omega))
updated_beta = 0.0
for i = 1:length(updated_omega)
updated_omega[i] = omega[i] - alpha * sum((1.0 ./ (1.0 + exp(-data * omega - beta)) - labels).* slice(data,:,i))
end
updated_beta = beta - alpha * sum((1.0 ./ (1.0 + exp(-data * omega - beta)) - labels))
return updated_omega, updated_beta
end
Naive maping results in high inefficiency. First of all please note that
(1.0 ./ (1.0 + exp(-data * omega - beta)) - labels)
is computed \(D+1\) times. Lets then compute it once before the for loop.
function update_params(omega::Array{Float64,2}, beta::Float64,data::Array{Float64,2}, labels::Array{Float64,1}, alpha::Float64)
updated_omega = zeros(Float64, length(omega))
updated_beta = 0.0
partial_derivative = (1.0 ./ (1.0 + exp(-data * omega - beta)) - labels)
for i = 1:length(updated_omega)
updated_omega[i] = omega[i] - alpha * sum(partial_derivative.* slice(data,:,i))
end
updated_beta = beta - alpha * sum(partial_derivative)
return updated_omega, updated_beta
end
Moreover for loop is not needed here. We can instead use basic linear algebra operation to replace it. Please note that at each iteration we compute the summation:
sum(partial_derivative.* slice(data,:,i))
First of all partial_derivative can be written as a row vector below
\[
\mathbf{f} = \begin{pmatrix}
(f(x_{1}, (\beta,\omega)) – y_{1}) & \cdots & (f(x_{N}, (\beta,\omega)) – y_{N})
\end{pmatrix}
\]
The summation under consideration is just a dot product between \(\mathbf{f}\) and \(X_{.i}\) (ith column of data matrix).
If you also note that
\[
\mathbf{f} X = \begin{pmatrix}
\mathbf{f} X_{.1} & \mathbf{f} X_{.2} & \cdots & \mathbf{f} X_{.N}
\end{pmatrix}
\]
then the for loop can be rewriten as
\[
\omega = \omega- \alpha \mathbf{f} X
\]
\[
\beta = \beta- \alpha \mathbf{f} \mathbf{1}
\]
where \(\mathbf{1}\) multiplication is just a convenient way of writing vector summation. Lets now finally write down update_params function
function update_params(omega::Array{Float64,2}, beta::Float64,data::Array{Float64,2}, labels::Array{Float64,1}, alpha::Float64)
partial_derivative = (1.0 ./ (1.0 + exp(-data * omega - beta))) - labels
omega = omega - alpha * (partial_derivative' * data)'
beta = beta - alpha * sum(partial_derivative)
return omega,beta
end
We can now compose all the puzzles together:
function predict(data, model_params)
1.0 ./ (1.0 + exp(-data * model_params[:omega] - model_params[:beta]))
end
function _mult(a::Array{Float64,1},b::Array{Float64,2})
result = zeros(length(a))
both_non_zero_indicator = ((a .!= 0) & (b .!= 0))
result[both_non_zero_indicator[:]] = a[both_non_zero_indicator[:]] .* b[both_non_zero_indicator]
return result
end
function goal_function(omega::Array{Float64,2}, beta::Float64, data::Array{Float64,2}, labels::Array{Float64,1})
f_partial = 1.0 ./ (1.0 + exp(-data * omega - beta))
result = -sum(_mult(labels, log(f_partial)) + _mult((1.0 - labels), log(1.0 - f_partial)))
return result
end
function convergence(omega::Array{Float64,2}, beta::Float64, data::Array{Float64,2}, labels::Array{Float64,1}, prevJ::Float64, epsilon::Float64)
currJ = goal_function(omega, beta, data, labels)
return abs(prevJ - currJ) < epsilon
end
function update_params(omega::Array{Float64,2}, beta::Float64,data::Array{Float64,2}, labels::Array{Float64,1}, alpha::Float64)
partial_derivative = (1.0 ./ (1.0 + exp(-data * omega - beta))) - labels
omega = omega - alpha * (partial_derivative' * data)'
beta = beta - alpha * sum(partial_derivative)
return omega,beta
end
function logistic_regression_learn(data::Array{Float64,2}, labels::Array{Float64,1}, params::Dict{Symbol,Float64})
omega = zeros(Float64, size(data,2),1)
beta = 0.0
J = Inf
current_iter = 0
alpha_step, epsilon, max_iter = params[:alpha], params[:eps], params[:max_iter]
while !convergence(omega, beta, data, labels, J, epsilon) && current_iter < max_iter
J = goal_function(omega, beta, data, labels)
omega, beta = update_params(omega, beta, data, labels, alpha_step)
current_iter += 1
end
model_params = Dict();
model_params[:omega] = omega; model_params[:beta] = beta;
return model_params
end
It is probably high time trying the code out but the post is getting too long. I think I will stop here and continue evaluation in the future.
But before that I think we now need some tools for visualization purposes. In the next post then I will try to install and play with Gadfly – visualization package for Julia.
To continue reading about logistic regression click here