Local Large Language Models

Posted May 31, 2023 Updated Jan 20, 2025

By Kamil

26 min read

Over the past few years, machine learning has become a bit daunting for regular folks. The coolest toys were being created by big companies with massive budgets, immense computational power, and the best talents in the world. Very often, the weights of the large models created by these big players were not disclosed, but rather bragged about in research papers/demo applications or exposed via paid API at best. Lots of regular individual researchers like myself happily training their humble models with scikit-learn soon realized it might be a bit hopeless trying to compete with that. The recent release of ChatGPT and GPT-4 seemed to be the final nail in the coffin.

Some recent breakthroughs sparked a light in that dark tunnel, though. It seems like with a bunch of tricks and hacks fine-tuning of Large Language Models can run even on everyday consumer hardware. In this blog post, we are going to go through the most visible bits contributing to that.

LoRA: Low-Rank Adaptation of Large Language Models

Large Language Models are models crafted to predict next “word” for given prefix of text (or prompt) – they are capable of understanding context and so producing text completion that not only makes sense but can be very precise to the extreme point of passing medical or law exams. The Famous GPT-4 and ChatGPT are both Large Language Models.

These Large Language Models are… large indeed, they can reach up to hundreds of billions of parameters. In its original form it is not possible to train/fine-tune any of these without hardly affordable cluster of GPUs.

(source: https://huggingface.co/blog/hf-bitsandbytes-integration)

Techniques presented in this blog post are addressing that limitation.

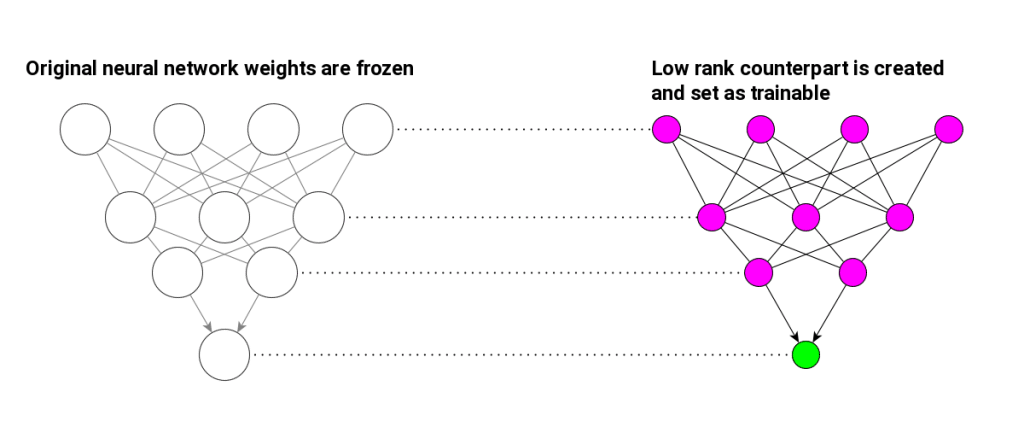
LoRA was introduced in 2021 by the researchers from Microsoft. It is a technique that lets you reduce number of trainable parameters during Large Language Models fine-tuning (but it’s not limited to LLMs). It achieves so by freezing original weights and injecting low rank trainable matrix deltas to original neural networks’ weights. These low rank matrices are defined as a product of two smaller matrices which implies much less trainable parameters.

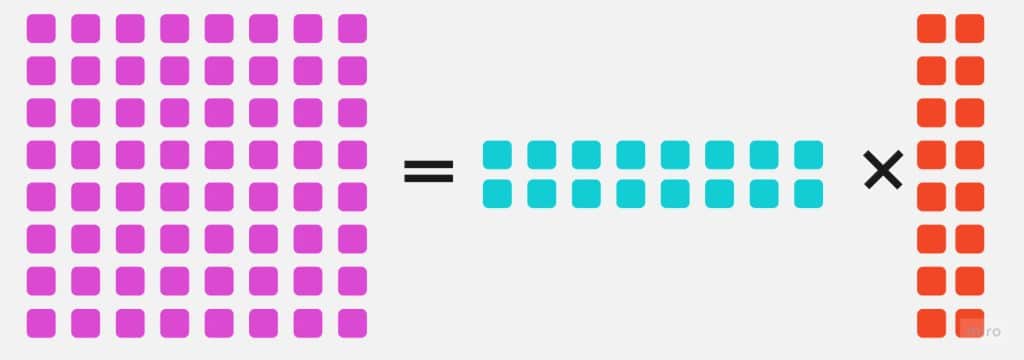(LoRA deltas are chosen to be a product of two smaller matrices)

Let’s see how low rank deltas are injected to one single linear layer weight matrix $W_0$.

As long as $B=0$, nothing can stop us from expressing our $W_{0}$ as:

\[W_0 = W_0 + \Delta{W} = W_{0} + AB\]

We basically added zero to an existing matrix – no big deal. Even though it is useless from algebra point of view, it is quite significant for the procedure of training a neural network. Because now we can freeze initial matrix $W_{0}$ – consider it constant and mark matrices $A$ and $B$ – which we can choose to be much smaller – as trainable. Gradients will be updated at matrices $A$ and $B$ only making them efficient proxy for model fine-tuning. Our huge original $W_{0}$ will remain unchanged.

LoRA does not apply low rank matrix approximation to neural network weights directly but rather inject trainable low-rank matrices that are added to original matrices

There is several advantages of such approach. You can choose which parameters of your initial huge LLM you want to update and add trainable $\Delta{W} = AB$ to those chosen parameters only.

LoRA is handy when you train several downstream tasks using the same base LLM – then you can share this base model among many downstream tasks at the same time (which also applies to inference).

LoRA in PEFT: State-of-the-art Parameter-Efficient Fine-Tuning

In addition to their research paper, the authors of LoRA released a very decent implementation of their approach as a Python package. A bit later, Hugging Face followed up and released PEFT – a general parameter-efficient fine-tuning library that includes LoRA as one of its techniques.

Let’s take a look at a very basic example of how to use LoRA with PEFT:

        
      
from transformers import AutoModelForSequenceClassification
from peft import get_peft_model, LoraConfig

roberta_for_sc = AutoModelForSequenceClassification.from_pretrained(
    "roberta-base",
)

config = LoraConfig(
    r=8,
    lora_dropout=0.1,
    lora_alpha=32,
    target_modules=['query', 'key', 'value']
)

peft_model = get_peft_model(
    roberta_for_sc,
    peft_config=config
)

peft_model.print_trainable_parameters()
# trainable params: 1034498 || 
# all params: 125089538 || 
# trainable%: 0.827006012285376

Line 3: Loading roberta-base model with a sequence classification downstream task in mind.
Line 7: LoRA config initialization.
- r sets the rank of $AB$ matrices about to be injected. It is set to 8 meaning that matrices $A$ and $B$ whenever injected next to original matrices will have fixed height and width set to 8, respectively.
- target_modules are the names of modules LoRA is applied to. Here it is set to query, key, and value which are the names of inner layers of self-attention layer from Transformer Architecture.
Line 12: Finally, PEFT model based on initial roberta-base model and LoRA config is created.

The very last line in the snippet above indicates trainable parameters got reduced to less than 1% of original size. This does not mean we are going to go 100x faster unfortunately. We still need to do full forward pass of original neural network. It is backward pass (back propagation step) where we save resources as gradients will only need updates at new trainable LoRA layers. In original paper authors report 25% speedup during training on GPT-3 175B compared to full fine-tuning and VRAM usage drop by up to 2/3.

Please note that LoRA will not bring much boost (if any) to single forward-pass/inference – however if several models share the same frozen original weights (imagine you train text-classification / question answering and NER based on the same base LLM) – it should be possible to speed up their inference together by caching and reusing precomputed outputs of frozen layers of the model.

LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale

The process of training and performing inference on neural networks relies heavily on matrix multiplication. The majority of the heavy computation done on GPUs involves multiplying one matrix by another. The storage requirement for each matrix is determined by its size and the precision of its entries, which is expressed in bytes required to store matrix weights. LoRA addresses the issue of the size of trainable matrices by approximating their deltas using low-rank counterparts. On the other hand, LLM.int8() is a technique that involves clever matrix multiplication using lower precision.

Original LLM.int8() paper was written in 2022 by Tim Dettmers. There is a supplementary amazing blog post describing the details of the technique.

Let’s focus on main building blocks of LLM.int8().

Absolute maximum 8-bit quantization

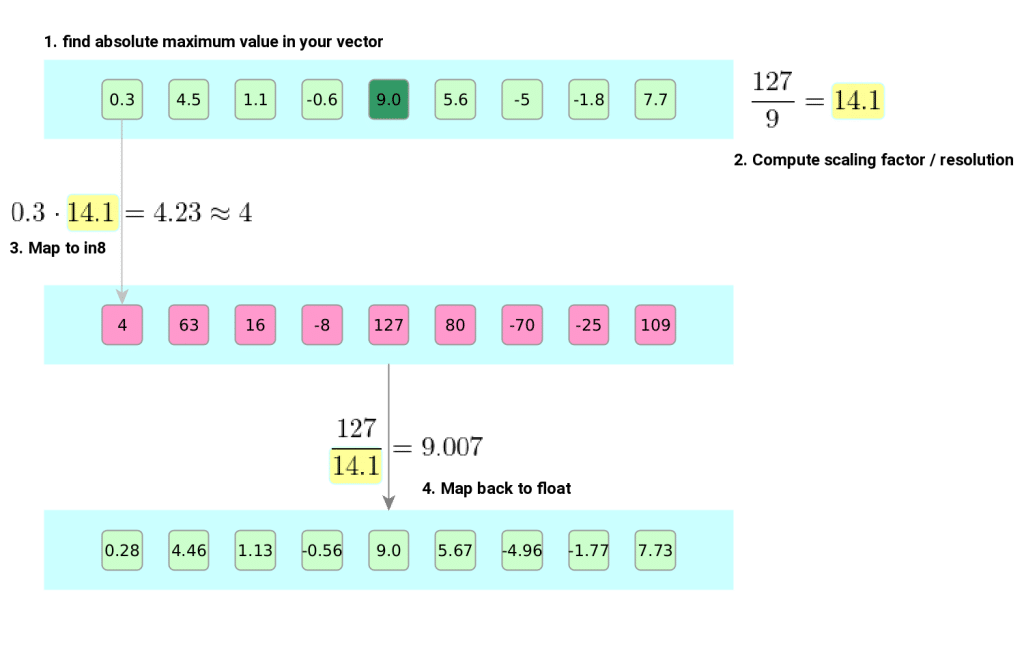
First bit to cover is absolute maximum 8-bit quantization which answers the question of how to represent vector/matrix/set of real numbers using 8 bits only (which covers 256 different values).

The procedure goes as follows: first step is to identify absolute maximum value in our vector $v$ at hand. This value is then used to compute scaling factor we are going to use to quantize and de-quantize our vector. Scaling factor is selected to make our absolute maximum value hit int8 boundary after quantization: $\frac{127}{\text{absmax}(v)}$. Second step is to multiply our vector element-wise with that scaling factor and round the results – this will map our vector to [-127,127] range (landing at int8 precision). De-quantization is done in a similar fashion using the same scaling factor – we divide int8 numbers with scaling factors to again land at float numbers.

LLM.int8() – Int8 matrix multiplication

The simplest approach to multiply two matrices using a technique presented above would be to quantize input matrices via single global scaling factor and multiply them as such. Unfortunately, absolute maximum 8-bit quantization is sensitive to outliers. Extreme example of problematic vector is $v = [0.3, 0.4, 0.5, 0.6, 512.0]$ which includes an outlier $512.0$. Scaling factor for this vector would be $0.24$ and so quantized vector would be $v_q = [0,0,0,0,1]$. Our outlier dominated lower values and made them indistinguishable. Probability of an outlier occurrence grows with the input size – therefore treating huge linear layer of Transformer as a single “block of numbers” with single scaling factor will most likely cause that issue. To lower that probability we need a clever partition of our matrices into blocks, each with different block-specific scaling factor.

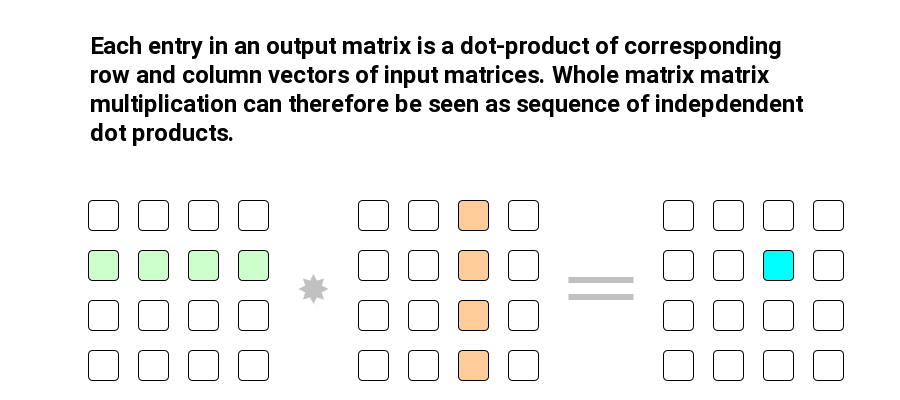
In order to grasp the reasoning behind blocking proposed by authors of LLM.int8() let’s recall that matrix matrix multiplication can be decomposed into sequence of inner products of rows and columns of the matrices involved.

With that decomposition in mind, the authors of LLM.int8() propose treating each row of an input matrix (features matrix) and each column of the weights matrix (hidden state matrix) as separate blocks, which are quantized independently.

Even this clever blocking crafted specifically for matrix multiplication is not free from outliers. These still exist and must be handled. To address this, the authors of the paper proposed treating any value with an absolute value greater than 6 as an outlier. Whenever a row/column with such a value is spotted, they do not quantize it, but rather produce the corresponding inner product using fp16 (16-bit floating point) precision – this is called mixed-precision decomposition scheme. This way, problematic outlier values are kept with high precision without interfering with the rest of the weights. The authors empirically show that using that blocking strategy plus handling outliers with fp16 precision yields close-to-zero degradation of the performance of Large Language Models. Moreover they note that more than 99.9% of values are still multiplied in efficient 8-bit.

The main advantage of using LLM.int8() is around 50% memory reduction compared to 16-bit.

LoRA requires potentially heavy forward pass through unchanged original base model weights – this is where LLM.int8() fits nicely, reducing memory requirements by half.

8-bit Optimizers via Block-wise Quantization

There is another less apparent area where GPU memory is heavily consumed – the optimizer states.

Broadly speaking, an optimizer is a function that consumes a neural network, a batch of input data, and a loss function as inputs, and outputs a neural network with updated weights. The modern optimizers demand additional memory as they need to store their previous state(s) to generate updated weights. For instance, Stochastic Gradient Descent (SGD) with momentum calculates weight updates as a linear combination of all historical updates forgetting its history exponentially.

Whenever you fine-tune a model using a modern optimizer you will need extra memory to store some historical weights updates, too. Modern optimizers use up to 75% of total memory used during training.

Tim Dettmers and his team addressed this issue by introducing 8-bit optimizers that use less memory to store their inner states.

Dynamic Tree Quantization

The core building block of 8-bit optimizers is dynamic tree quantization. Similar to absolute max quantization dynamic tree quantization is a yet another way of representing a vector/matrix/set of float numbers with 8 bits only.

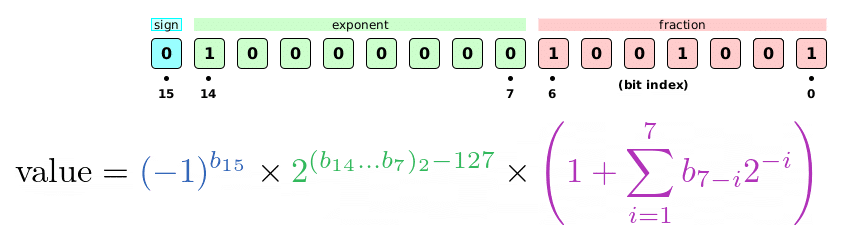
Before going into details of dynamic tree quantization let’s go through a simple exercise and try to understand another floating point representation – Brain Floating Point or bfloat16 in short. This will be our reference we will compare dynamic tree quantization with.

(Brain Floating Point)

Brain Floating Point is packed in 16 bits. First bit is a sign bit indicating sign of the final number, the following 8 bits are exponent bits which tell us the magnitude range our final number falls in. The last 7 bits are fraction bits – they yield actual precision our number will follow. The number above is:

\[\text{value} = 1 \cdot 2 \cdot \left(1 + \frac{1}{2} + \frac{1}{16} + \frac{1}{128}\right) = 3.140625\]

Brain Floating Point has a fixed structure – first bit always represents a sign, consecutive 8 bits always represent exponent and the following 7 bits represent a fraction. In that sense Brain Floating Point representation is static.

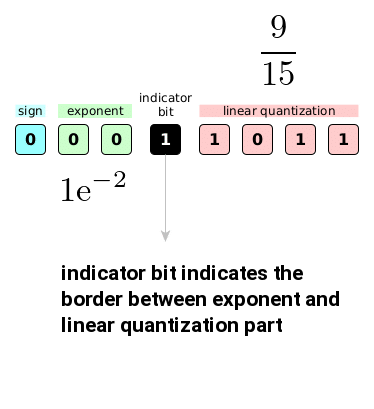
Dynamic Tree Quantization is different on many levels. It uses 8 bits to represent the numbers and it is not static as bfloat16 – the indicator bit dynamically determines exponent and linear quantization sizes. It is designed to represent numbers from [-1,1] range too. Let’s take a look at interpretation of Dynamic Tree Quantization below:

First bit indicates the sign of the final number, the number of consecutive zeros after that will yield an exponent and the next bit is a flag bit that marks the end of exponent part. The remaining bits contribute to the final number via linear quantization component (also known as “binary bisection tree”)

The example number above is computed in the following way

\[\text{value} = 1 \cdot e^{-2} \cdot \frac{9}{15} = 0.08120\]

Authors also introduced a variant of dynamic tree quantization called dynamic quantization – this variant is specifically crafted for Adam optimizer where one of the internal states stored by Adam is positive and so it does not require sign bit. That bit is then used in “linear quantization” part instead.

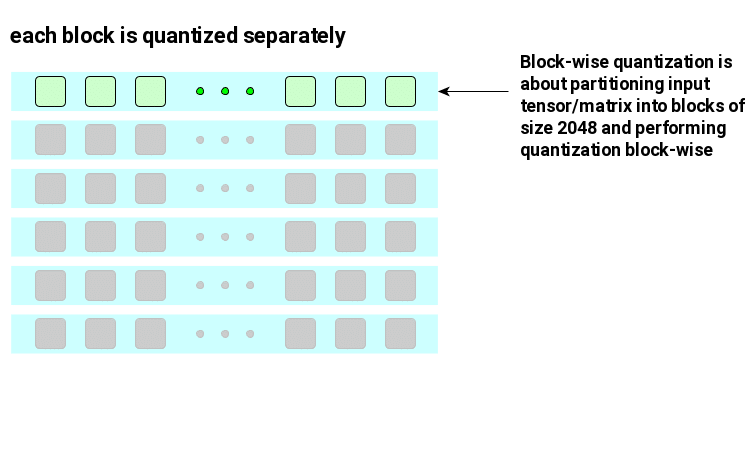
Block-wise quantization

Block-wise quantization is about clever partitioning of input optimizer state tensor/matrix. It is essentially addressing the same issue we saw in case of LLM.int8() related to precision degradation of underlying quantization caused by outliers. With block-wise partitioning strategy, outliers effects are reduced to a single block – not entire tensor/matrix.

For 8bit optimizers, a block size is set to 2048. Except of handling outliers such choice is related to the underlying dynamic tree quantization process which requires block normalization to a range of (-1, 1). If the entire tensor needed normalization, all cores would have to be engaged in the computation. However, with block-wise partitioning, normalization can be performed independently on each core.

Stable Embedding Layer

Last bit introduced by authors of “8-bit Optimizers via Block-wise Quantization” is Stable Embedding Layer – crafted for NLP tasks specifically. Authors noticed that using classical embedding layer leads to instability of 8bit optimizers presented above. They decided to patch it by proposing Stable Embedding Layer which – as authors admit themselves – is simply a new composition of previously known ideas.

Bitsandbytes: 8-bit CUDA functions for PyTorch

All the ideas presented above: LLM.int8() and 8-bit optimizers are implemented in a python package called bitsandbytes and moreover they are integrated with Hugging Face, meaning that you can load any model from the model hub and mark it as 8bit, any forward pass will then be performed via LLM.int8(). You can also use bitsandbytes 8bit optimizer and use it in hugging face Trainer class.

Let’s take a look at the LLM.int8() in action below:

How to use LLM.int8() in Hugging Face?

This is regular text generation code using RedPajama-INCITE-Chat-3B-v1 model. The only unusual bit in case of 8bit model is load_in_8bit flag that does all the magic for free. It will convert weight matrices into their 8bit quantized approximations and imply LLM.int8() matrix multiplication for them.

        
      
import torch
import transformers
from transformers import AutoModelForCausalLM

model_16bit = AutoModelForCausalLM.from_pretrained(
    "togethercomputer/RedPajama-INCITE-Chat-3B-v1",
    torch_dtype=torch.float16
)
model_16bit = model_16bit.to("cuda:0")

model_8bit = AutoModelForCausalLM.from_pretrained(
    "togethercomputer/RedPajama-INCITE-Chat-3B-v1",
    torch_dtype=torch.float16, 
    load_in_8bit=True, 
    device_map="auto"
)   
print(
  "model_8bit requires "
  f"{round(model_8bit.get_memory_footprint() / 1024**3,2)} G"
)

print(
  "model_16bit requires "
  f"{round(model_16bit.get_memory_footprint() / 1024**3,2)} G"
)

The memory required to store RedPajama-INCITE-Chat-3B-v1 using 8bit is 2.95G while original model requires 5.3G

Hugging Face is now integrated with bitsandbytes, using just a single flag load_in_8bit when loading the model will imply int8 weight matrices and LLM.int8() matrix multiplication for free – lowering memory requirements by almost half

How to use 8bit optimizers in Hugging Face?

8bit optimizers can be used with hugging face, too. It is as easy as passing it explicitly to Trainer.

This is an example of roberta-base fine tuning with 8bit optimizer in action. Please be aware this is toy example and some extra steps need to be taken in order to successfully fine-tune NLP model with 8-bit optimizer – using StableEmbedding layer is one of them.

8bit optimizers from bitsandbytes is compatible with Trainer, meaning that you can use it interchangeable with other classical 32bit optimizers from torch.optim module.

        
      
from datasets import load_dataset
from transformers import AutoTokenizer
from transformers import AutoModelForSequenceClassification
from transformers import TrainingArguments, Trainer 
import bitsandbytes as bnb 
import torch 

dataset = load_dataset("yelp_review_full")
tokenizer = AutoTokenizer.from_pretrained(
    "roberta-base"
)

def tokenize_function(examples):
    return tokenizer(
        examples["text"], 
        padding="max_length", 
        truncation=True
    )

tokenized_datasets = dataset.map(tokenize_function, batched=True)
small_train_dataset = tokenized_datasets["train"].shuffle(
    seed=42).select(range(1000))
small_eval_dataset = tokenized_datasets["test"].shuffle(
    seed=42).select(range(1000))

model = AutoModelForSequenceClassification.from_pretrained(
    "roberta-base", 
    num_labels=5, 
    device_map="auto"
)

training_args = TrainingArguments(
    "output_dir", 
    per_device_train_batch_size=24
)

optimizer_8bit = bnb.optim.Adam8bit(
    model.parameters()
)

trainer = Trainer(
    model=model,
    args=training_args,
    train_dataset=small_train_dataset,
    eval_dataset=small_eval_dataset,
    optimizers=(optimizer_8bit, None)
)
trainer.train()

4bit quantization – GPTQ / GGML

While 8bit quantization seems to be extreme already, there are even more hardcore quantization regimes out there. One of the most popular is GPTQ – introduced in March 2023 which uses 4 bits (16 distinct values!) to represent a floating point.

GPTQ is post-training quantization method crafted specifically for GPT (Generative Pretrained Transformers) models. GPTQ tries to solve an optimization problem for each layer separately.

Let’s take a look at this optimization problem closely. The setup is the following: we have single linear layer of original model we are about to quantize and its corresponding weight matrix $W$ at hand, we also have a small amount of $m$ example inputs organized in a matrix $X$. We are after 4bit matrix $\hat{W}$ that solves:

\[\text{argmin}_{\hat{W}} || WX – \hat{W}X ||\]

which expresses the simple goal of finding 4bit version of weights matrix such that for given set of input data $X$ it yields the results that are closest to original weight matrix.

Authors solve the following problem using modified Optimal Brain Quantization method. The details of the technique are a bit involved and go much beyond the scope of this (too long already) post, though.

The corresponding code can be found in github repository complementary to the paper. Another related repository that is worth looking at is https://github.com/ggerganov/ggml which is designed to support CPU and offers 4bit quantization (using slightly different technique) as well.

QLoRA = Quantization + LoRA

Another great contribution from Tim Dettmers is, just recently introduced, QLoRA – which is a composite of LoRA and clever 4bit quantization for the application of efficient fine-tuning.

One of the core components of QLoRA is the 4-bit NormalFloat Quantization, a method for compressing matrix weights into a 4-bit representation. This representation expresses 16 distinct values (4^2) and is designed to yield uniform distribution over bin counts that each 4-bit vector represents, making 4-bit NormalFloat an information-theoretically optimal data type.

The next trick is Double Quantization which is the process of quantization of quantization constants. Block size of 4-bit NormalFloat Quantization is small enough for it to actually makes sense.

In QLoRA, only the frozen weights of the base LoRA model are 4-bit quantized, while the weights of the LoRA matrices (deltas) are kept in BrainFloat16. During both the forward and backward passes, the 4-bit weights are dequantized to bfloat16, and computations are performed using the bfloat16 data type.

QLoRA significantly reduces the memory requirement for fine-tuning large language models, lowering the bar by an additional 50% and allowing even larger models to be trained locally. This makes 33-billion parameter models trainable on GPUs with 24GB of VRAM.

The authors of QLoRA have also introduced a model called Guanaco, trained using QLoRA, which is currently considered one of the best locally available LLMs (though this status changes frequently, so it’s best not to stick to it too much).

QLoRA is being merged into Hugging Face, and soon, we can expect a load_in_4bit=True flag to be added to HF, similar to what we have already seen with LLM.int8().

Instruction Fine Tuning

Another big field that contributes to the progress around LLMs is related to data itself. People come up with ideas of how to craft training data for LLMs which implies their future applications, behavior or if you will “thinking”. We have multilingual datasets, domain-specific datasets, dialog oriented datasets and many more.

It has been demonstrated that LLMs benefits from fine-tuning against datasets specifically crafted to follow instructions and solving tasks. Using such datasets for LLM fine-tuning is called “instruction fine-tuning”. ChatGPT and its “open-source” alternatives were all fine-tuned that way.

Instruction fine-tuning is process of fine-tuning language models on a collection of datasets described via instructions/tasks

In FLAN paper (which is the one introducing the idea) instructions were composed from tens of existing datasets by applying predefined task templates. For example entries from IMDB review (originally represented as text with binary target: positive/negative) could be transformed into the following tasks:

For each of the datasets authors proposed bunch of such templates and produced their huge diverse dataset. Model fine tuned this way is known as FLAN-T5 and is available on HF model hub.

The approach described above requires human manual work which introduces a bias but also may become a bottleneck. To limit that effect researchers went step forward and started utilizing existing LLMs to generate instructions for them.

Self-Instruct

One of the very first approaches for LLM aided instructions generation is presented in Self-Instruct paper. Self-Instruct aim is to automatically produce LLM fine-tuning dataset using LLM itself.

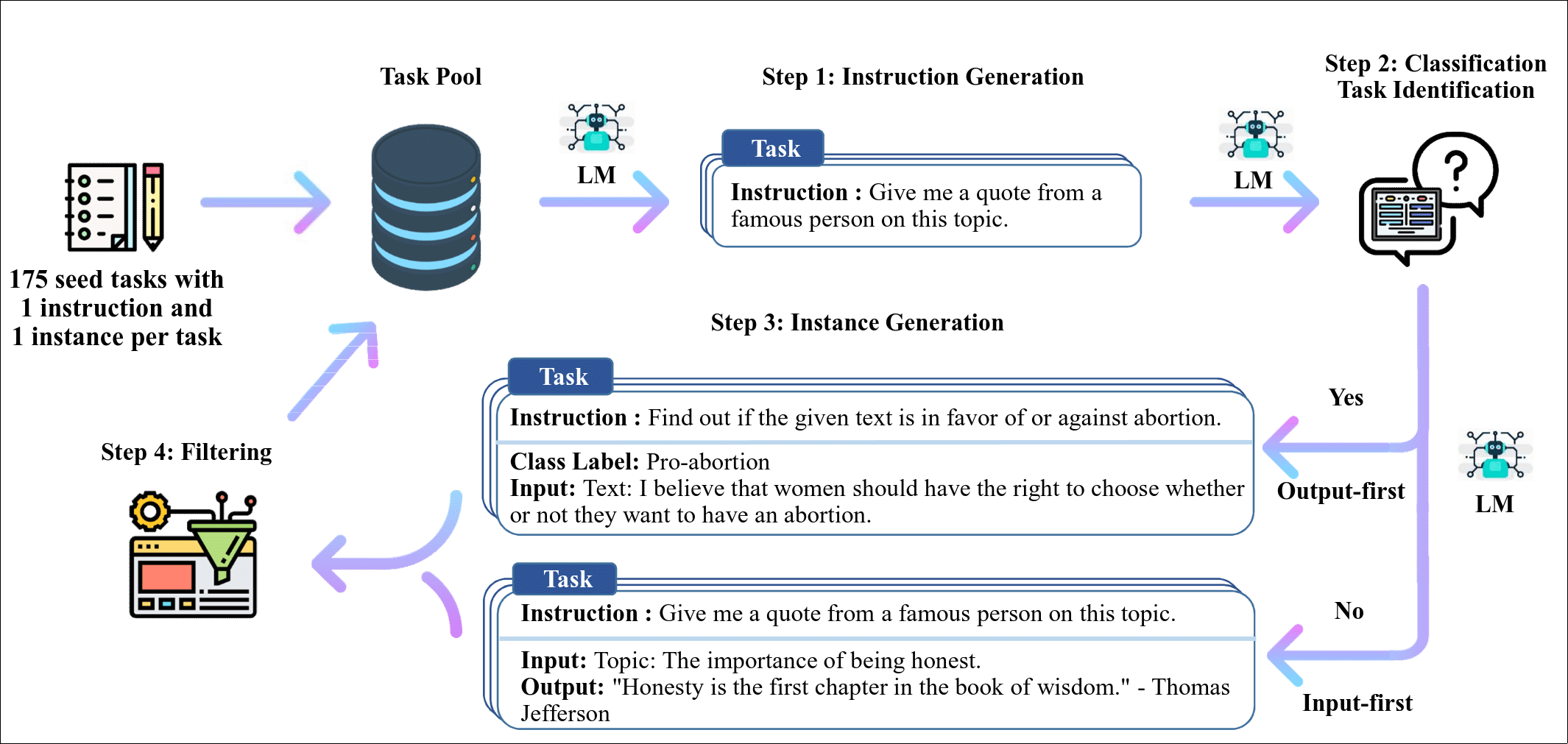
The high-level overview of the described Self-Instruct approach is depicted on the image below:

Authors distinguish two types of tasks: “classification tasks” and “non-classification tasks“. The pipeline starts with human generated small tasks seed. Then 4 consecutive automatic steps are performed:

Instruction Generation

LLM is prompted to produce set of tasks similar to the 8 tasks selected from the pool (6 artificial + 2 human-generated). Prompt sent to LLM looks as follows:

New tasks are produced until max length is reached or task 16 is generated.
Classification Task Identification

The next step is to figure out the type of newly generated tasks. Again LLM is prompted with set of existing tasks we know the type of and asked about new task type:
Instance Generation

Authors propose to use two different approaches to generate “answers” to the tasks produced so far depending on task type at hand. For non-classification tasks they propose Input-First Approach with example prompt below:

For classification tasks they use Output-First Approach with corresponding prompt example like:
Filtering

The very last step before tasks generated in (1,2,3) end up in task pool is filtering. Authors accept the tasks with ROUGE-L less than 0.7 (to encourage diversity in final dataset). Additionally they exclude tasks with keywords from a predefined set (like images, pictures, graphs, ++).

Except of datasets automatically created with LLMs like the ones we presented above, there are datasets carefully created by humans like OpenAssistant or collected by online community like ShareGPT.

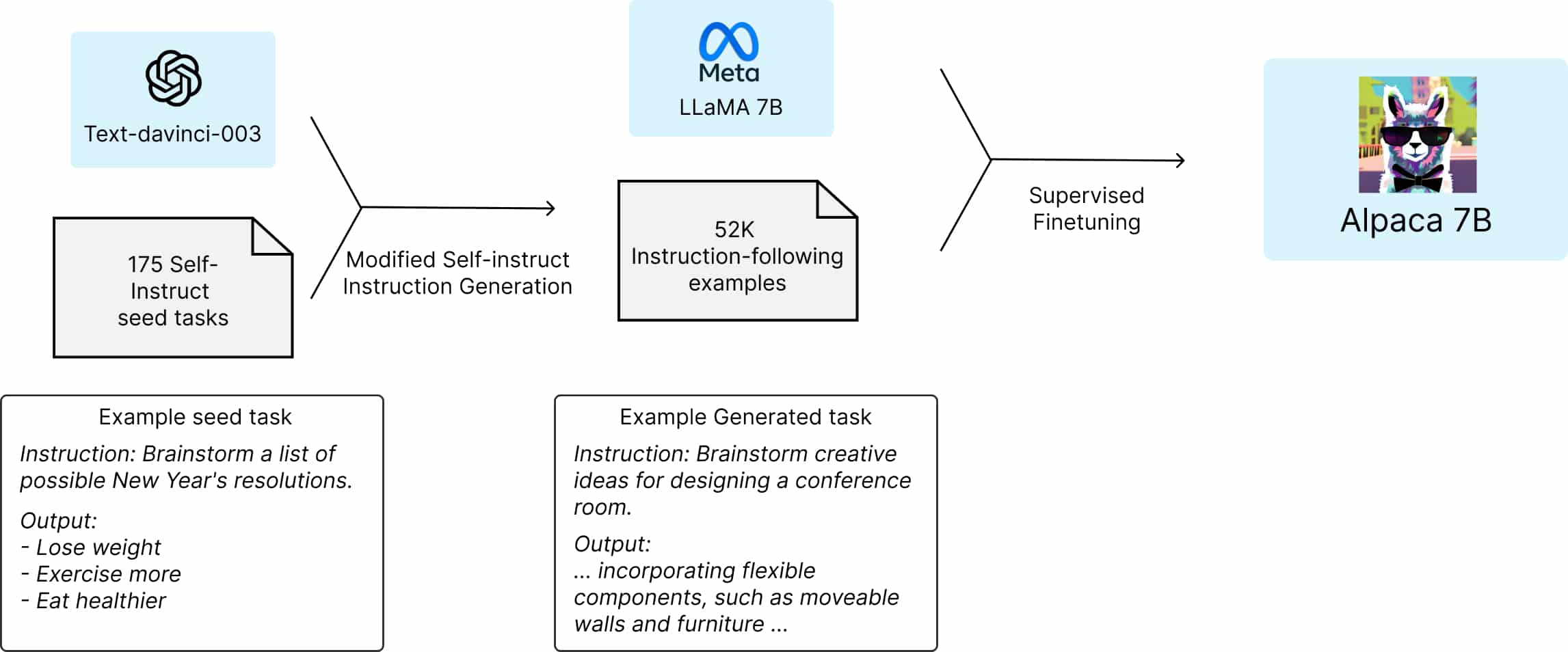
Stanford Alpaca

Not long after the Self-Instruct paper, a follow-up project was run by researchers at Stanford – Stanford Alpaca. This time, both the dataset and the code used to generate it were open-sourced and published on GitHub. The authors utilized the OpenAI text-davinci-003 model as an LLM and made slight modifications to the prompts as well. The resulting model, trained on the Stanford Alpaca dataset, is known as Alpaca 7B, with some of its variations being publicly available.

Evol-Instruct

The next big thing that emerged was Evol-Instruct which is yet another method for producing large amount of diverse instructions for instruction fine-tuning without human supervision. Evol-Instruct starts with a single instruction and evolves it through two type of operations: In-depth Evolving with the purpose of making currently given instructions more complex and increase their difficulty level and In-Breadth Evolving which focuses on increasing the topic coverage, skill coverage, and overall diversity of the existing instruction dataset. Then the dataset filtered by Elimination Evolving which filters out responses classified as failure. All these operations are performed by LLM fed with carefully crafted prompts.

Local LLMs

LoRA/QLoRA, model weight quantization, and well-designed instruction fine-tuning datasets significantly contribute to the development of local/private LLMs – Large Language Models that can be hosted on consumer hardware. We will now go through the most popular models (as for June 23):

Alpaca-LoRA

Alpaca-LoRA, released in March 2023, was developed with the objective of replicating the Alpaca Stanford results utilizing LoRA. This resulted in two key artifacts: the fine-tuned LLM with 7B parameters, and the corresponding efficient fine-tuning routine. Under the hood, Alpaca-LoRA employs LoRA along with 8-bit quantization (aka LLM.int8()). The LLama model serves as the base starting point for it. Alpaca-LoRA was trained using the Alpaca Stanford dataset, and you can interact with it here.

Vicuna

The next big thing coming weeks after was Vicuna which is fine-tuned LLama fine-tuned on 70K user-shared conversations gathered from sharegpt.com. Here neither LoRA nor quantization was used for fine-tuning, however the authors managed to keep the training cost below 300 USD. They used gradient checkpointing and flash attention to reduce memory and, consequently, the cost. The models are available on huggingface model hub.

Dolly 2.0

Databricks brought Dolly 2.0 to the spotlight as the first fully open-source model. Dolly uses Pythia as a base model and a dataset of 15k human-generated instructions. Both model and dataset are available for commercial use under Apache 2.0.

OpenAssistant

The OpenAssistant project, organized by LAION, aims to make chatbot technology accessible to everyone. The project has released bunch of models fine-tuned on human-crafted instructions, which users can contribute to through the Open Assistant web UI. The current models created by the OpenAssistant community include those based on Llama, Pythia and StableLM.

MosaicPretrainedTransformer (MPT) models

In May 2023, MPT (MosaicML Pretrained Transformer) models family have been presented with one significant release MPT-base 7B. Trained on one trillion tokens, this model is available for commercial use under the Apache 2.0 license, making it an attractive option for businesses. Authors claim performance close to Llama7B.

WizardLM

WizardLM is model created by researchers from Microsoft and Peking University. It is Llama based model presenting capabilities of Evol-Instruct – method utilizing LLM to construct instructions for instruction fine-tuning. Except of the dataset itself, authors released the models weights deltas (that you can add to Llama weights) on hugging face.

Guanaco

The most recent star is Guanaco – the result of Llama fine-tuned with QLoRA. Guanaco is revolutionary as it reduced memory requirements by half because of 4bit quantization used during training. The smallest Guanaco model (7B) uses ~5 GB of memory while performing significantly better than Alpaca model (26 GB memory requirement) on the Vicuna test by more than 20 percentage points. The biggest Guanaco has 65B parameters but it still can fit into 41 GB GPU VRAM. It also achieves the best performance, comparable to ChatGPT on the Vicuna benchmark.

The base LLM model – an elephant in the room

Unfortunately, there is still a cold shower in store for those caught up in the unlimited “open source” LLM euphoria – the lack of a truly open-source base LLM. Many of the most powerful models aiming to compete with ChatGPT rely on Meta’s Llama base model, which is not available for commercial use and is not open. Currently, there is no single clear open alternative, although there are attempts and ambitious plans in progress.

Stability AI, the team behind Stable Diffusion, is working on an open-source LLM initiative under the project named StableLM. Additionally, there is the Pythia model family, as well as OpenLlama, which is trained on the RedPajama dataset containing more than 1 trillion tokens and aims to reproduce the dataset used for Llama training. Falcon-40B is a somewhat “open” model with its own catch-22 for commercial use – it is free until you make 1 million USD per year.

The current direction is very promising, and it seems likely that we will see the development of fully open-source LLMs in the near future. However, the reality is that this area is currently facing a commercial bottleneck.

Summary

In conclusion, Large Language Models have gone through quite some development recently. It’s difficult to determine if we are to witness a true revolution in this field soon – opinions on that matter are more belief-based than knowledge-based. However, it is important to note that AI has come close to groundbreaking advancements many times in the past, such as with symbolic AI (Prolog, expert systems) in the 1980s. Yet, so far, the anticipated “Terminator-like” scenario has not arrived.

What is undoubtedly true are the measurable tools now available that allow running LLMs on local machines, lowering the entry barrier for researchers and creating an excellent environment for further development.

Tags: large language models, LoRA, natural language processing, neural networks, quantization

Large Language Models

This post is licensed under CC BY 4.0 by the author.